트리 순회(Tree Traversal)
1. 트리 순회?
트리의 노드들을 한번씩만 방문(하여 탐색)하는 방법을 말한다.
트리 순회의 방법은 크게 DFS와 BFS로 나뉜다.
DFS에서는 Pre, In, Post - Order 의 세가지 방법으로 또다시 나뉜다.
1-1. 트리의 DFS
트리의 DFS(Depth First Search)는 트리의 레벨 별로 보다 높이쪽을 먼저 공략하는 방식이다.
이진 트리의 경우 DFS는 루트(서브 트리의 루트), 왼쪽 자식, 오른쪽 자식 중 어떤 것을 먼저 방문하느냐에 따라 pre, in, post 방식으로 다시 나뉜다. 이 때 기준이 되는 것은 루트이다. 예를들어 루트를 가장 먼저 방문하는 순회방식은 pre-order(전위 순회)라고 하고, 루트를 중간에 방문하는 것을 in-order(중위 순회), 루트를 마지막에 방문하는 것은 post-order(후위 순회)라고 한다.
(DFS는 깊이를 타고 계속 들어가기 때문에, in-order를 예로 들면, 왼쪽 자식->루트->오른쪽 자식 이렇게 바로바로 방문될 수 없다. 왼쪽 자손 -> 마지막 자손의 루트 -> 마지막 자손의 루트의 오른쪽 자식 -> .... -> 왼쪽 자식 -> 루트 -> .... 이렇게 진행되게 된다.)
1-2. 트리의 BFS
트리의 BFS(Breadth First Search)는 각 레벨을 순회한 후에 다음 레벨을 순회하는 방법이다. 레벨 순서 순회(Level-Order Traversal)이라고도 한다.
2. 구현
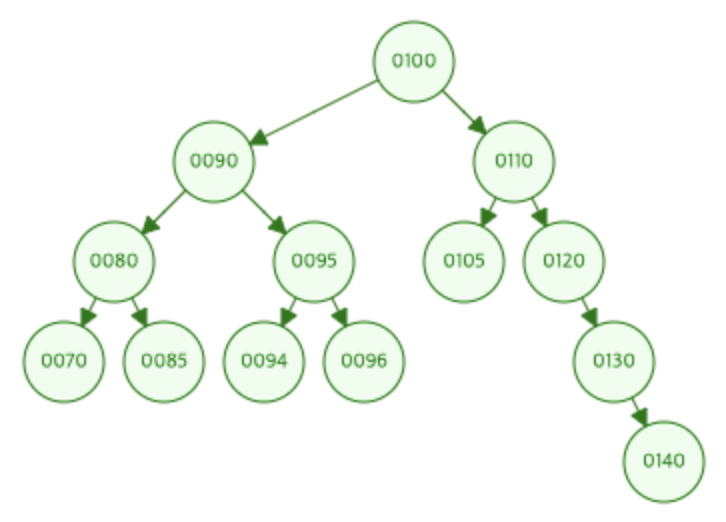
트리 노드 데이터 클래스와 테스트할 트리의 구조는 아래와 같다.
트리 노드 데이터
data class TreeNode (
var left: TreeNode? = null,
var right: TreeNode? = null,
val key: Int
) {
companion object {
fun getDummyTree(): TreeNode {
val node100 = TreeNode(key = 100)
val node90 = TreeNode(key = 90)
val node80 = TreeNode(key = 80)
val node70 = TreeNode(key = 70)
val node85 = TreeNode(key = 85)
val node95 = TreeNode(key = 95)
val node94 = TreeNode(key = 94)
val node96 = TreeNode(key = 96)
val node110 = TreeNode(key = 110)
val node105 = TreeNode(key = 105)
val node120 = TreeNode(key = 120)
val node130 = TreeNode(key = 130)
val node140 = TreeNode(key = 140)
node100.left = node90
node100.right = node110
node90.left = node80
node90.right = node95
node80.left = node70
node80.right = node85
node95.left = node94
node95.right = node96
node110.left = node105
node105.right = node120
node120.right = node130
node130.right = node140
return node100
}
}
}
테스트 트리
2-1. DFS 구현 - Pre-Order (전위 순회)
재귀 사용
class TreeTraversal {
//...
fun preOrderUsingRecursive(root: TreeNode?) {
if (root == null) return
print("${root.key}, ")
root.left?.let {
preOrderUsingRecursive(root.left)
}
root.right?.let {
preOrderUsingRecursive(root.right)
}
}
}
스택 사용
class TreeTraversal {
fun preOrderUsingStack(root: TreeNode?) {
val stack: Stack<TreeNode> = Stack()
stack.push(root)
while (!stack.empty()) {
val curNode = stack.pop()
print("${curNode.key}, ")
curNode.right?.let {
stack.push(it)
}
curNode.left?.let {
stack.push(it)
}
}
}
//...
}
테스트
fun main(args: Array<String>) {
val traversal = TreeTraversal()
val tree = TreeNode.getDummyTree()
traversal.preOrderUsingStack(tree) // 100, 90, 80, 70, 85, 95, 94, 96, 110, 105, 120, 130, 140,
println("\n-----------------------")
traversal.preOrderUsingRecursive(tree) // 100, 90, 80, 70, 85, 95, 94, 96, 110, 105, 120, 130, 140,
}
2-2. DFS 구현 - In-Order(중위 순회)
재귀 사용
class TreeTraversal {
//...
fun inOrderUsingRecursive(root: TreeNode?) {
if (root == null) return
root.left?.let {
inOrderUsingRecursive(root.left)
}
print("${root.key}, ")
root.right?.let {
inOrderUsingRecursive(root.right)
}
}
//...
}
스택 사용
스택을 사용할 때에 왼쪽 서브트리의 루트들을 모두 담아야 하기 때문에 while문이 while문 안에 들어가게 된다. 이후에는 루트의 오른쪽 노드의 왼쪽 서브트리를 다시 순회하게 구현한다.
class TreeTraversal {
//...
fun inOrderUsingStack(root: TreeNode?) {
if (root == null) return
val stack: Stack<TreeNode> = Stack()
var curNode: TreeNode? = root
while(curNode != null || !stack.empty()) {
while(curNode != null) {
stack.push(curNode)
curNode = curNode.left
}
curNode = stack.pop()
print("${curNode.key}, ")
curNode = curNode.right
}
}
//...
}
테스트
fun main(args: Array<String>) {
val traversal = TreeTraversal()
val tree = TreeNode.getDummyTree()
traversal.inOrderUsingStack(tree) // 70, 80, 85, 90, 94, 95, 96, 100, 105, 110, 120, 130, 140,
println("\n-----------------------")
traversal.inOrderUsingRecursive(tree) // 70, 80, 85, 90, 94, 95, 96, 100, 105, 110, 120, 130, 140,
}
2-3. DFS 구현 - Post-Order(후위 순회)
재귀 사용
class TreeTraversal {
//...
fun postOrderUsingRecursive(root: TreeNode?) {
if (root == null) return
root.left?.let {
postOrderUsingRecursive(root.left)
}
root.right?.let {
postOrderUsingRecursive(root.right)
}
print("${root.key}, ")
}
//...
}
스택 사용
스택을 사용하기 위해서는 pop한 노드의 오른쪽 서브트리를 순회하였는지를 확인해야 한다. 오른쪽 서브트리를 모두 순회하지 않았다면 아직 해당 노드는 pop되면 안되기 때문에 다시 push해주는 작업이 필요하다.
class TreeTraversal {
//...
fun postOrderUsingStack(root: TreeNode?) {
if (root == null) return
val stack: Stack<TreeNode> = Stack()
val visitedRightNode: MutableSet<TreeNode> = mutableSetOf()
var curNode: TreeNode? = root
while(curNode != null || !stack.empty()) {
while(curNode != null) {
stack.push(curNode)
curNode = curNode.left
}
val tempNode = stack.pop()
if (tempNode.right != null && !visitedRightNode.contains(tempNode.right)) {
visitedRightNode.add(tempNode.right!!)
stack.push(tempNode)
curNode = tempNode.right
} else {
print("${tempNode.key}, ")
}
}
}
//...
}
테스트
fun main(args: Array<String>) {
val traversal = TreeTraversal()
val tree = TreeNode.getDummyTree()
traversal.postOrderUsingStack(tree) // 70, 85, 80, 94, 96, 95, 90, 105, 140, 130, 120, 110, 100,
println("\n-----------------------")
traversal.postOrderUsingRecursive(tree) // 70, 85, 80, 94, 96, 95, 90, 105, 140, 130, 120, 110, 100,
}
2-4. BFS 구현
큐 사용
class TreeTraversal {
//...
fun bfs(root: TreeNode?) {
if (root == null) return
val queue: Queue<TreeNode> = LinkedList()
queue.offer(root)
while (!queue.isEmpty()) {
val curNode = queue.poll()
print("${curNode.key}, ")
curNode.left?.let {
queue.offer(it)
}
curNode.right?.let {
queue.offer(it)
}
}
}
//...
}
테스트
fun main(args: Array<String>) {
val traversal = TreeTraversal()
val tree = TreeNode.getDummyTree()
traversal.bfs(tree) // 100, 90, 110, 80, 95, 105, 120, 70, 85, 94, 96, 130, 140,
}